[AI와 QA의 만남] - Study Day2 (학습일: ‘20.04.21)

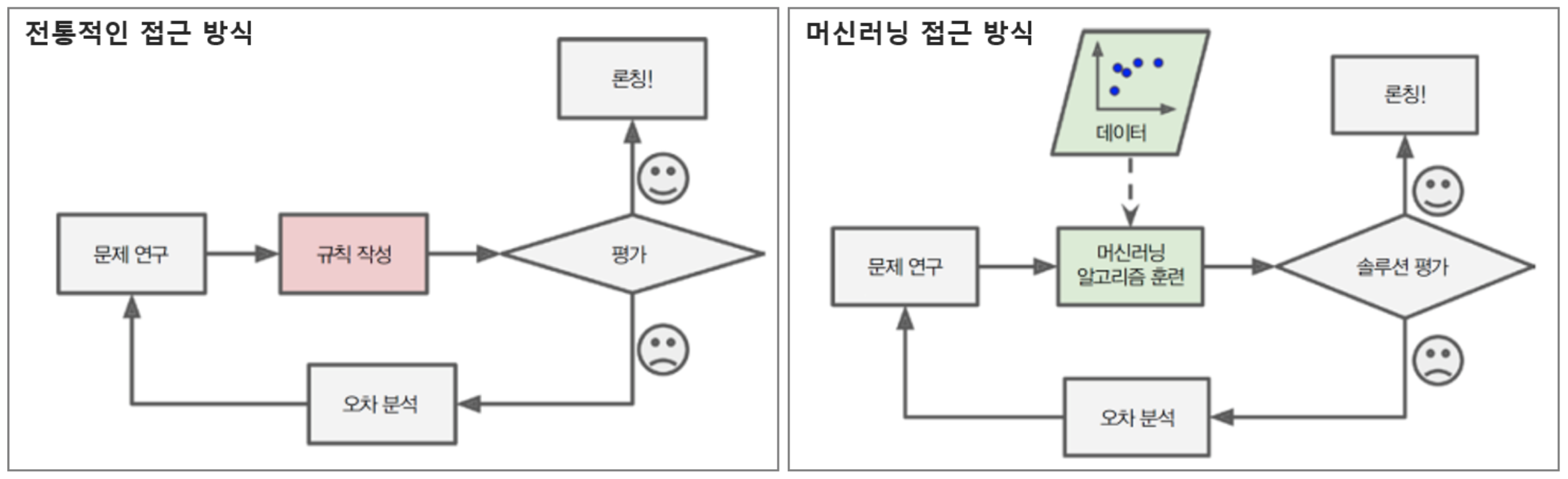
Wrap-up : 전통적 프로그래밍 접근방식 vs. 머신러닝 접근방식

프로그래밍 접근 방식

사람의 뉴런으로부터 딥러닝까지

아래 이미지들은 https://www.slideshare.net/JinWonLee9/ss-70446412 이진원 님의 슬라이드쉐어 자료에서 가져왔습니다.

  • 뉴런과 사람의 학습

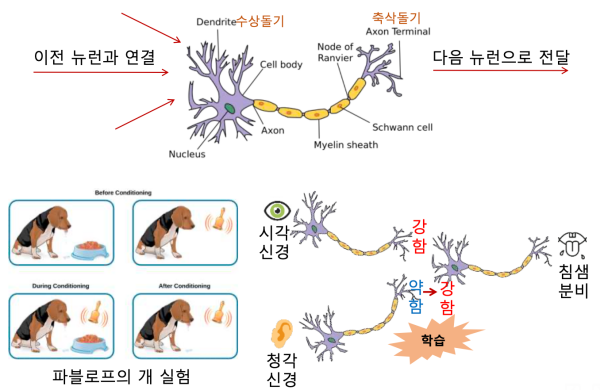
    뉴런의 학습

    • 뉴런의 학습에 의해 입력 신호에 따라 출력 신호의 강도가 달라진다.
    • 이전 뉴런의 출력 신호는 다음 뉴런으로 전달된다.

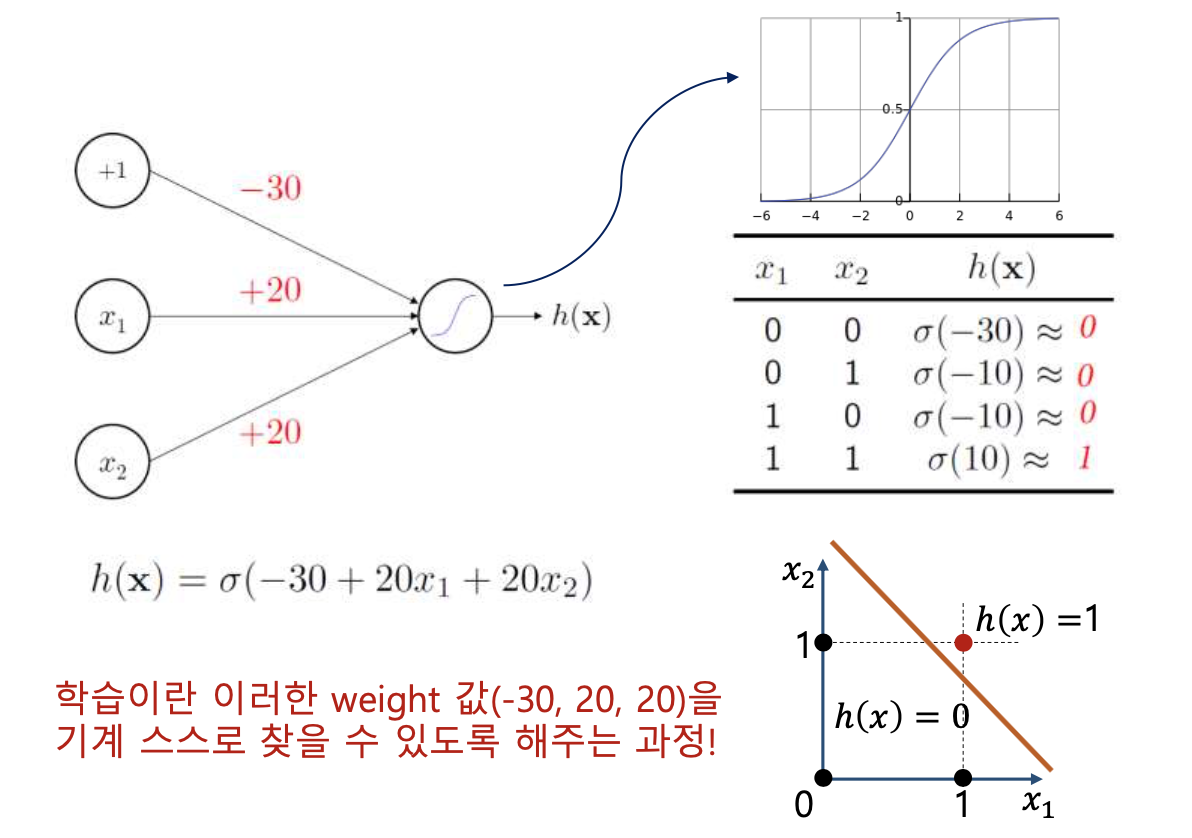
  • 퍼셉트론(Perceptron, Artificial Neural Network)

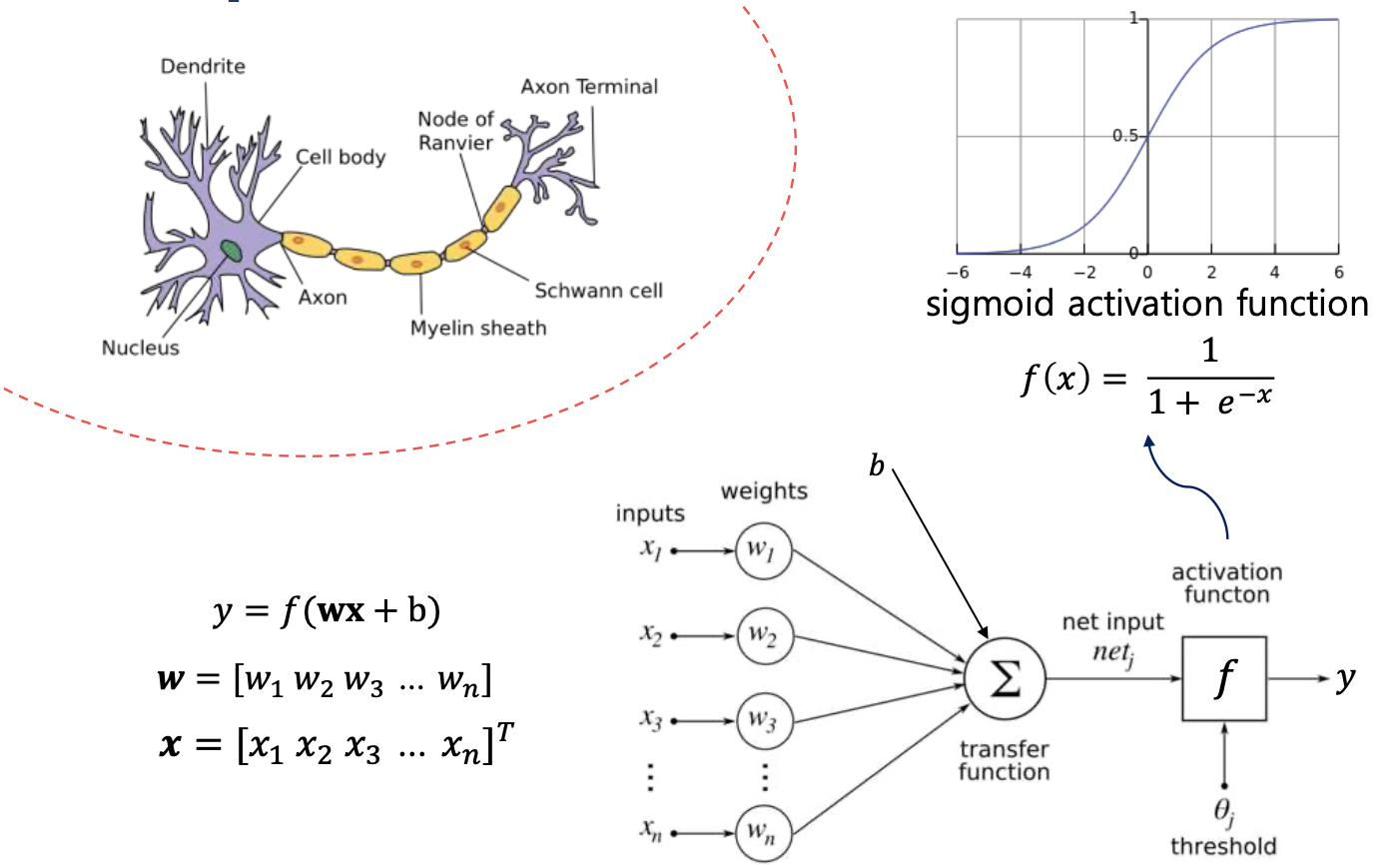
    Perceptron

    • Perceptron은 사람의 Neuron을 본따서 만든 가장 간단한 인공신경망 모델이다.
    • 입력 신호에 가중치를 곱하고, 그것들을 합한 후 일정한 Threshold를 넘으면 Y에 값이 출력된다.

  • 활성화 함수 : Sigmoid

    Sigmoid

    • 출력 값이 Threshold를 넘어서는지 판단하기 위해 사용하는 함수가 활성화 합수이며, 초창기에는 Sigmoid 함수(S자 모양의 함수)를 사용했다.
    • 활성화 함수는 1차 함수를 사용하면 Layer(층)을 Deep 하게 쌓는 의미가 없다.

  • 딥러닝

    dnn

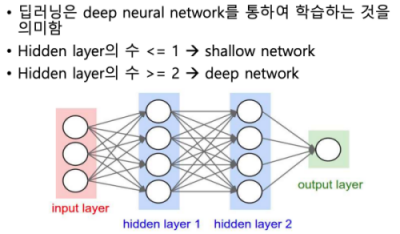
    • Deep Learning은 Deep Neural Network을 통하여 학습하는 것을 의미한다.
    • Hidden Layer 수가 2 이상인 경우를 딥러닝이라 한다.
    • 노드 간을 연결하는 각 라인이 하나의 파라미터를 가지고 있으므로, 층이 깊게 할수록 학습해야 할 가중치(Weight)가 많아진다.

  • Gradient Descent & Back Propagation

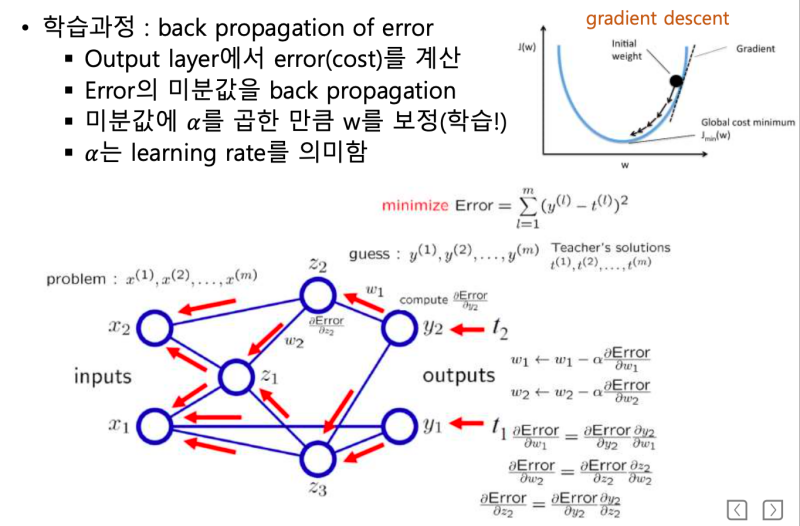
    Back Propagation

    • 손실 함수를 사용하여 가중치(Weight)를 조정한다. 손실 함수를 미분하여 기울기를 계산하고, 기울기가 0에 가까워지는 방향으로 가중치를 조정(+ or -) 한다. 이 방법을 경사하강법(Gradient Descent) 이라 한다.
    • Y의 예측값으로 부터 입력 데이터 방향으로 모든 가중치 값을 경사하강법을 사용하여 조정한다. 이 과정을 오차역전파(Back Propagation of Error)라 한다.

  • Vanishing Gradient 문제

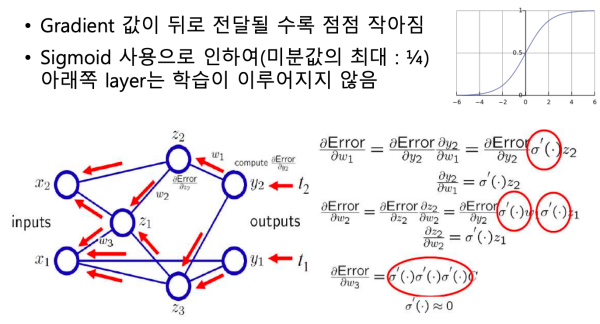
    Vanishing Gradient

    • Layer(층)이 깊어지는 경우 오차역전파법으로 반복적으로 미분 하면 기울기가 소실되어 가중치 값이 잘 갱신되지 않는 Vanishing Gradient(기울기 소실) 문제가 발생한다.

  • ReLU(Rectified Linear Unit)

    ReLU

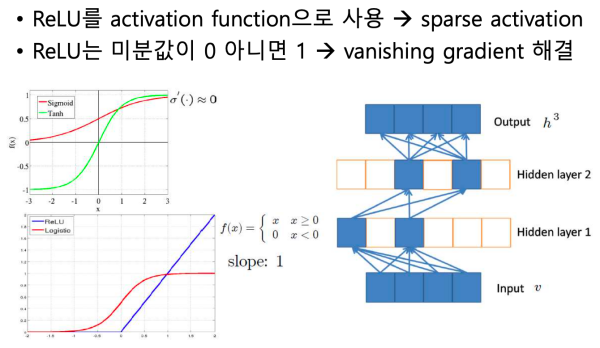
    • 활성화 함수로 Sigmoid 대신 ReLU를 사용 해서, Back Propagation(오차역전파법)에서 기울기가 소실되는 문제를 해결했다.

딥너닝의 작동 원리

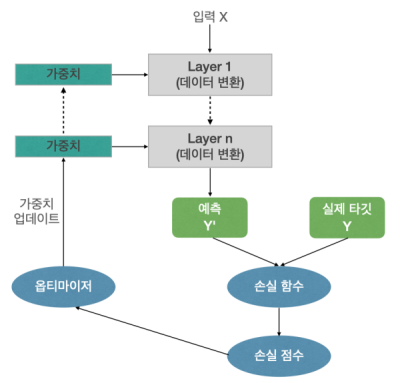
딥러닝 작동 원리

  • 신경망은 가중치를 파라미터로 가진다. (초기 가중치는 랜덤하게 정한다. 초기 가중치를 지정하는 다양한 알고리즘이 있다.)
  • 손실 함수로 신경망의 출력 품질을 측정한다. (예측값과 실제 타깃값을 비교하여 손실 점수를 계산한다.)
  • 손실 점수를 피드백 신호로 사용하여 손실 점수를 조정한다. (손실 점수가 작아지는 방향으로 가중치를 조정한다.)